Journal Description
Symmetry
Symmetry
is an international, peer-reviewed, open access journal covering research on symmetry/asymmetry phenomena wherever they occur in all aspects of natural sciences. Symmetry is published monthly online by MDPI.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), CAPlus / SciFinder, Inspec, Astrophysics Data System, and other databases.
- Journal Rank: JCR - Q2 (Multidisciplinary Sciences) / CiteScore - Q1 (General Mathematics)
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 14.7 days after submission; acceptance to publication is undertaken in 3.7 days (median values for papers published in this journal in the first half of 2023).
- Recognition of Reviewers: reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any MDPI journal, in appreciation of the work done.
- Sections: published in 6 topical sections.
- Testimonials: See what our editors and authors say about Symmetry.
Impact Factor:
2.7 (2022);
5-Year Impact Factor:
2.7 (2022)
Latest Articles
Modelling Symmetric Ion-Acoustic Wave Structures for the BBMPB Equation in Fluid Ions Using Hirota’s Bilinear Technique
Symmetry 2023, 15(9), 1682; https://doi.org/10.3390/sym15091682 (registering DOI) - 01 Sep 2023
Abstract
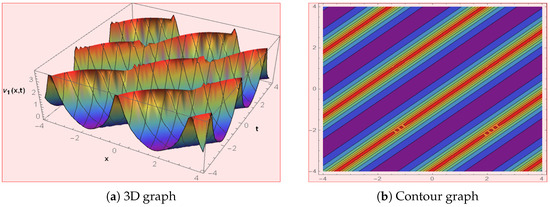
This paper investigates the ion-acoustic wave structures in fluid ions for the Benjamin–Bona–Mahony–Peregrine–Burgers (BBMPB) equation. The various types of wave structures are extracted including the three-wave hypothesis, breather wave, lump periodic, mixed-type wave, periodic cross-kink, cross-kink rational wave, M-shaped rational wave, M-shaped rational
[...] Read more.
This paper investigates the ion-acoustic wave structures in fluid ions for the Benjamin–Bona–Mahony–Peregrine–Burgers (BBMPB) equation. The various types of wave structures are extracted including the three-wave hypothesis, breather wave, lump periodic, mixed-type wave, periodic cross-kink, cross-kink rational wave, M-shaped rational wave, M-shaped rational wave solution with one kink wave, and M-shaped rational wave with two kink wave solutions. The Hirota bilinear transformation is a powerful tool that allows us to accurately find solutions and predict the behaviour of these wave structures. Through our analysis, we gain a better understanding of the complex dynamics of ion-acoustic waves and their potential applications in various fields. Moreover, our findings contribute to the ongoing research in plasma physics that utilize ion-acoustic wave phenomena. To show the physical behaviour of the solutions, some 3D plots and their respective contour level are shown, choosing different values of the parameters.
Full article
(This article belongs to the Section Mathematics and Symmetry/Asymmetry)
►
Show Figures
Open AccessArticle
Accelerated Subgradient Extragradient Algorithm for Solving Bilevel System of Equilibrium Problems
by
and
Symmetry 2023, 15(9), 1681; https://doi.org/10.3390/sym15091681 (registering DOI) - 31 Aug 2023
Abstract
In this research paper, we propose a novel approach termed the inertial subgradient extragradient algorithm to solve bilevel system equilibrium problems within the realm of real Hilbert spaces. Our algorithm is capable of circumventing the necessity for prior knowledge about the Lipschitz constant
[...] Read more.
In this research paper, we propose a novel approach termed the inertial subgradient extragradient algorithm to solve bilevel system equilibrium problems within the realm of real Hilbert spaces. Our algorithm is capable of circumventing the necessity for prior knowledge about the Lipschitz constant of the involving bifunction and only computes the minimization of strong bifunctions onto the feasible set that is required. Under appropriate conditions, we establish strong convergence theorems for our proposed algorithms. To validate our algorithms, we illustrate a series of numerical examples. Through these examples, we demonstrate the performance of the algorithms we have put forth in this paper.
Full article
(This article belongs to the Special Issue Symmetry in Fixed Point Approaches and Nonlinear Functional Mathematical Equations)
►▼
Show Figures
Figure 1
Open AccessArticle
q-Rung Orthopair Fuzzy Archimedean Aggregation Operators: Application in the Site Selection for Software Operating Units
Symmetry 2023, 15(9), 1680; https://doi.org/10.3390/sym15091680 (registering DOI) - 31 Aug 2023
Abstract
The q-rung orthopair fuzzy (q-ROF) set is an efficient tool for dealing with uncertain and inaccurate data in real-world multi-attribute decision-making (MADM). In MADM, aggregation operators play a significant role. The majority of well-known aggregation operators are formed using algebraic,
[...] Read more.
The q-rung orthopair fuzzy (q-ROF) set is an efficient tool for dealing with uncertain and inaccurate data in real-world multi-attribute decision-making (MADM). In MADM, aggregation operators play a significant role. The majority of well-known aggregation operators are formed using algebraic, Einstein, Hamacher, Frank, and Yager t-conorms and t-norms. These existing t-conorms and t-norms are some special cases of Archimedean t-conorms (ATCNs) and Archimedean t-norms (ATNs). Therefore, this article aims to extend the ATCN and ATN operations under the q-ROF environment. In this paper, firstly, we present some new operations for q-ROF sets based on ATCN and ATN. After that, we explore a few desirable characteristics of the suggested operational laws. Then, using these operational laws, we develop q-ROF Archimedean weighted averaging (geometric) operators, q-ROF Archimedean order weighted averaging (geometric) operators, and q-ROF Archimedean hybrid averaging (geometric) operators. Next, we develop a model based on the proposed aggregation operators to handle MADM issues. Finally, we elaborate on a numerical problem about site selection for software operating units to highlight the adaptability and dependability of the developed model.
Full article
(This article belongs to the Special Issue Recent Advances in Fuzzy Optimization Methods and Models)
►▼
Show Figures
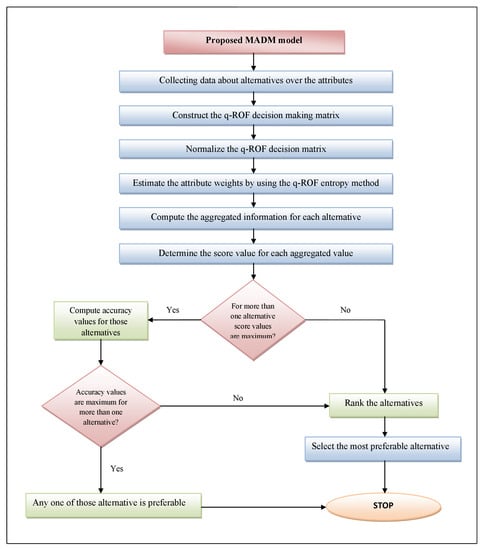
Figure 1
Open AccessReview
A Systematic Literature Review on Identifying Patterns Using Unsupervised Clustering Algorithms: A Data Mining Perspective
by
, , , , and
Symmetry 2023, 15(9), 1679; https://doi.org/10.3390/sym15091679 - 31 Aug 2023
Abstract
Data mining is an analytical approach that contributes to achieving a solution to many problems by extracting previously unknown, fascinating, nontrivial, and potentially valuable information from massive datasets. Clustering in data mining is used for splitting or segmenting data items/points into meaningful groups
[...] Read more.
Data mining is an analytical approach that contributes to achieving a solution to many problems by extracting previously unknown, fascinating, nontrivial, and potentially valuable information from massive datasets. Clustering in data mining is used for splitting or segmenting data items/points into meaningful groups and clusters by grouping the items that are near to each other based on certain statistics. This paper covers various elements of clustering, such as algorithmic methodologies, applications, clustering assessment measurement, and researcher-proposed enhancements with their impact on data mining thorough grasp of clustering algorithms, its applications, and the advances achieved in the existing literature. This study includes a literature search for papers published between 1995 and 2023, including conference and journal publications. The study begins by outlining fundamental clustering techniques along with algorithm improvements and emphasizing their advantages and limitations in comparison to other clustering algorithms. It investigates the evolution measures for clustering algorithms with an emphasis on metrics used to gauge clustering quality, such as the F-measure and the Rand Index. This study includes a variety of clustering-related topics, such as algorithmic approaches, practical applications, metrics for clustering evaluation, and researcher-proposed improvements. It addresses numerous methodologies offered to increase the convergence speed, resilience, and accuracy of clustering, such as initialization procedures, distance measures, and optimization strategies. The work concludes by emphasizing clustering as an active research area driven by the need to identify significant patterns and structures in data, enhance knowledge acquisition, and improve decision making across different domains. This study aims to contribute to the broader knowledge base of data mining practitioners and researchers, facilitating informed decision making and fostering advancements in the field through a thorough analysis of algorithmic enhancements, clustering assessment metrics, and optimization strategies.
Full article
(This article belongs to the Special Issue Symmetry or Asymmetry in Machine Learning)
Open AccessArticle
Application of Graphene Oxide–Natural Polymer Composite Adsorption Materials in Water Treatment
by
Symmetry 2023, 15(9), 1678; https://doi.org/10.3390/sym15091678 - 31 Aug 2023
Abstract
Graphene is a new type of carbon material with excellent properties that has been developed in recent years. Graphene composites have potential application value in solving the problem of water pollution. In this study, we investigated the properties and performance of graphene composites
[...] Read more.
Graphene is a new type of carbon material with excellent properties that has been developed in recent years. Graphene composites have potential application value in solving the problem of water pollution. In this study, we investigated the properties and performance of graphene composites prepared through polymer modification and inorganic particle doping modification. Our research focused on the composites’ ability to adsorb heavy metal ions and degrade organic compounds through photocatalysis. In this study, we prepared graphene oxide (GO) first and then grafted p-phenylenediamine onto its surface. The process was successful and yielded promising results. The aniline grafted onto the graphene oxide surface was used as anchor point for the in situ redox polymerization of aniline, and a polyaniline macromolecular chain was grafted onto the edge of graphene oxide. The structure of the composite was determined using Fourier transform infrared spectroscopy, thermogravimetry, X-ray diffraction, and Raman spectroscopy and transmission electron microscopy. The adsorption performance of Pb+ on GO-PANI composite was studied. The maximum adsorption capacity of the GO-PANI composite for Pb+ is 1416 mg/g, 2.3 times that of PANI. Graphene/polyaniline composites can be used as an excellent adsorbent for Pb2+ heavy metal ions and have great application prospects in heavy metal wastewater treatment.
Full article
(This article belongs to the Special Issue Applications of Nanomaterials Beyond the Boundaries of Symmetry)
►▼
Show Figures
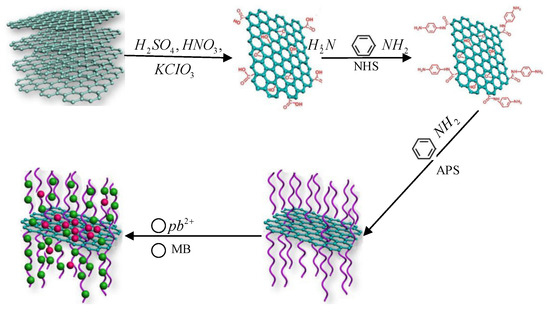
Figure 1
Open AccessArticle
Generalized Polynomials and Their Unification and Extension to Discrete Calculus
Symmetry 2023, 15(9), 1677; https://doi.org/10.3390/sym15091677 - 31 Aug 2023
Abstract
In this paper, we introduce a comprehensive and expanded framework for generalized calculus and generalized polynomials in discrete calculus. Our focus is on
In this paper, we introduce a comprehensive and expanded framework for generalized calculus and generalized polynomials in discrete calculus. Our focus is on
(This article belongs to the Special Issue Symmetries of Difference Equations, Special Functions and Orthogonal Polynomials II)
Open AccessArticle
Total Perfect Roman Domination
Symmetry 2023, 15(9), 1676; https://doi.org/10.3390/sym15091676 - 31 Aug 2023
Abstract
A total perfect Roman dominating function (TPRDF) on a graph
A total perfect Roman dominating function (TPRDF) on a graph
(This article belongs to the Special Issue Symmetry and Graph Theory)
►▼
Show Figures
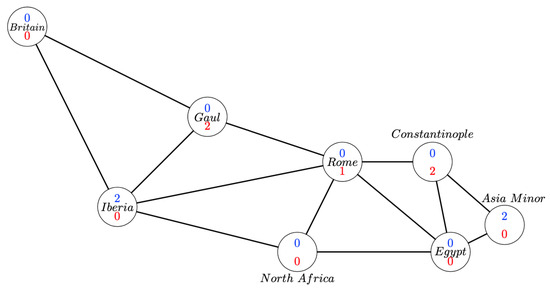
Figure 1
Open AccessArticle
The Chen Autoregressive Moving Average Model for Modeling Asymmetric Positive Continuous Time Series
Symmetry 2023, 15(9), 1675; https://doi.org/10.3390/sym15091675 - 31 Aug 2023
Abstract
In this paper, we introduce a new dynamic model for time series based on the Chen distribution, which is useful for modeling asymmetric, positive, continuous, and time-dependent data. The proposed Chen autoregressive moving average (CHARMA) model combines the flexibility of the Chen distribution
[...] Read more.
In this paper, we introduce a new dynamic model for time series based on the Chen distribution, which is useful for modeling asymmetric, positive, continuous, and time-dependent data. The proposed Chen autoregressive moving average (CHARMA) model combines the flexibility of the Chen distribution with the use of covariates and lagged terms to model the conditional median response. We introduce the CHARMA structure and discuss conditional maximum likelihood estimation, hypothesis testing inference along with the estimator asymptotic properties of the estimator, diagnostic analysis, and forecasting. In particular, we provide closed-form expressions for the conditional score vector and the conditional information matrix. We conduct a Monte Carlo experiment to evaluate the introduced theory in finite sample sizes. Finally, we illustrate the usefulness of the proposed model by exploring two empirical applications in a wind-speed and maximum-temperature time-series dataset.
Full article
(This article belongs to the Section Mathematics and Symmetry/Asymmetry)
►▼
Show Figures
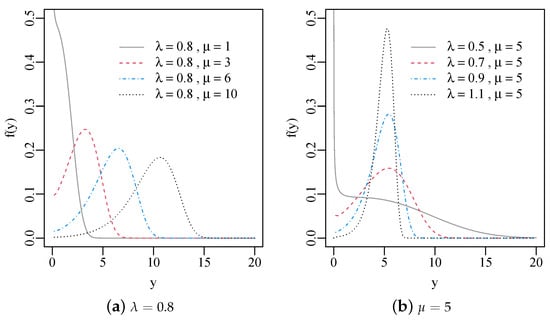
Figure 1
Open AccessArticle
On Hankel and Inverse Hankel Determinants of Order Two for Some Subclasses of Analytic Functions
Symmetry 2023, 15(9), 1674; https://doi.org/10.3390/sym15091674 - 30 Aug 2023
Abstract
In view of the subclass
In view of the subclass
(This article belongs to the Special Issue Symmetry in Geometric Theory of Analytic Functions)
Open AccessArticle
Joint Optimization Scheme of User Association and Channel Allocation in 6G HetNets
by
, , , and
Symmetry 2023, 15(9), 1673; https://doi.org/10.3390/sym15091673 - 30 Aug 2023
Abstract
The sixth-generation (6G) wireless cellular network integrates several wireless bands and modes with the objectives of improving quality of service (QoS) and increasing network connectivity. The 6G environment includes asymmetrical heterogeneous networks (HetNets) with the intention of making effective use of the available
[...] Read more.
The sixth-generation (6G) wireless cellular network integrates several wireless bands and modes with the objectives of improving quality of service (QoS) and increasing network connectivity. The 6G environment includes asymmetrical heterogeneous networks (HetNets) with the intention of making effective use of the available frequencies. However, selecting a suitable gNB and a communication channel that works for users in the network is an enormous challenge in 6G HetNets. This paper investigates a joint user association (UA) and channel allocation (CA) problem in two-tier HetNets by considering the downlink scenario to improve QoS. Our study presents an innovative scheme for user association and channel allocation, wherein the user can be connected to either the macro base station (MBS) or a possible small base station (SBS) in a direct or relay-assisted link. Furthermore, the proposed scheme identifies the optimal channel to be allocated to each user so that the overall network QoS can be maximized. A symmetric matching game-based user association is proposed to find the optimal association for users. Moreover, a modified auction game is applied to allocate the optimal channel by considering the quota of each gNB. Regarding connection probability, throughput, energy efficiency (EE), and spectrum efficiency (SE), the simulation results show that the proposed approach performs well over the state-of-the-art techniques.
Full article
(This article belongs to the Special Issue Technical Challenges and Symmetries in Next Generation Mobile Networks)
►▼
Show Figures
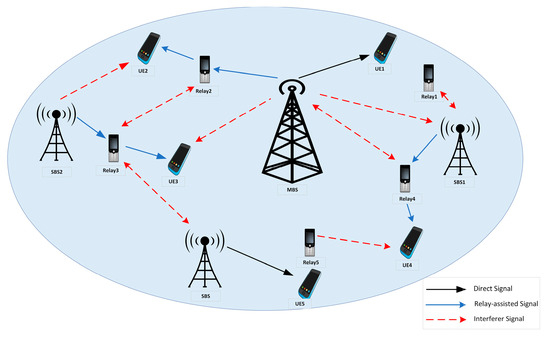
Figure 1
Open AccessArticle
Quaternion Quantum Mechanics II: Resolving the Problems of Gravity and Imaginary Numbers
Symmetry 2023, 15(9), 1672; https://doi.org/10.3390/sym15091672 - 30 Aug 2023
Abstract
We present a quaternion representation of quantum mechanics that allows its ontological interpretation. The correspondence between classical and quaternion quantum equations permits one to consider the universe (vacuum) as an ideal elastic solid. Elementary particles would have to be standing or soliton-like waves.
[...] Read more.
We present a quaternion representation of quantum mechanics that allows its ontological interpretation. The correspondence between classical and quaternion quantum equations permits one to consider the universe (vacuum) as an ideal elastic solid. Elementary particles would have to be standing or soliton-like waves. Tension induced by the compression and twisting of the elastic medium would increase energy density, and as a result, generate gravity forcing and affect the wave speed. Consequently, gravity could be described by an index of refraction.
Full article
(This article belongs to the Special Issue Symmetry and Asymmetry in Quantum Mechanics)
►▼
Show Figures
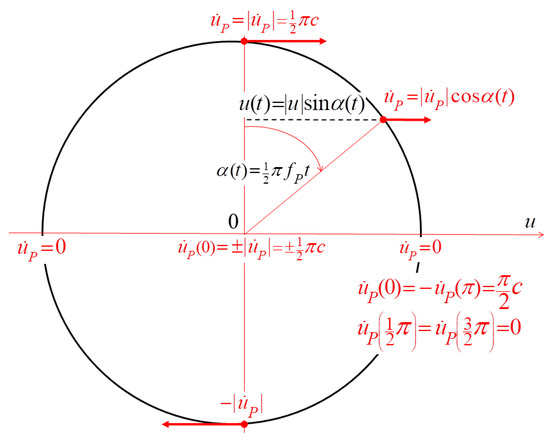
Figure 1
Open AccessArticle
Reliability Analysis of Kavya Manoharan Kumaraswamy Distribution under Generalized Progressive Hybrid Data
Symmetry 2023, 15(9), 1671; https://doi.org/10.3390/sym15091671 - 30 Aug 2023
Abstract
Generalized progressive hybrid censoring approaches have been developed to reduce test time and cost. This paper investigates the difficulties associated with estimating the unobserved model parameters and the reliability time functions of the Kavya Manoharan Kumaraswamy (KMKu) distribution based on generalized type-II progressive
[...] Read more.
Generalized progressive hybrid censoring approaches have been developed to reduce test time and cost. This paper investigates the difficulties associated with estimating the unobserved model parameters and the reliability time functions of the Kavya Manoharan Kumaraswamy (KMKu) distribution based on generalized type-II progressive hybrid censoring using classical and Bayesian estimation techniques. The frequentist estimators’ normal approximations are also used to construct the appropriate estimated confidence intervals for the unknown parameter model. Under symmetrical squared error loss, independent gamma conjugate priors are used to produce the Bayesian estimators. The Bayesian estimators and associated highest posterior density intervals cannot be derived analytically since the joint likelihood function is provided in a complicated form. However, they may be evaluated using Monte Carlo Markov chain (MCMC) techniques. Out of all the censoring choices, the best one is selected using four optimality criteria.
Full article
(This article belongs to the Special Issue Symmetrical and Asymmetrical Distributions in Statistics and Data Science)
►▼
Show Figures

Figure 1
Open AccessArticle
Exact Boundary Correction Methods for Multivariate Kernel Density Estimation
by
Symmetry 2023, 15(9), 1670; https://doi.org/10.3390/sym15091670 - 30 Aug 2023
Abstract
This paper develops a method to obtain multivariate kernel functions for density estimation problems in which the density function is defined on compact support. If domain-specific knowledge requires certain conditions to be satisfied at the boundary of the support of an unknown density,
[...] Read more.
This paper develops a method to obtain multivariate kernel functions for density estimation problems in which the density function is defined on compact support. If domain-specific knowledge requires certain conditions to be satisfied at the boundary of the support of an unknown density, the proposed method incorporates the information contained in the boundary conditions into the kernel density estimators. The proposed method provides an exact kernel function that satisfies the boundary conditions, even for small samples. Existing methods primarily deal with a one-sided boundary in a one-dimensional problem. We consider density in a two-sided interval and extend it to a multi-dimensional problem.
Full article
(This article belongs to the Special Issue Nonparametric Statistics and Biostatistical Methods)
►▼
Show Figures
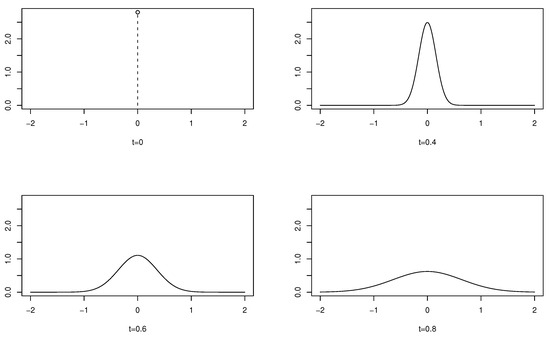
Figure 1
Open AccessArticle
Laplace-Domain Hybrid Distribution Model Based FDIA Attack Sample Generation in Smart Grids
Symmetry 2023, 15(9), 1669; https://doi.org/10.3390/sym15091669 - 30 Aug 2023
Abstract
False data injection attack (FDIA) is a deliberate modification of measurement data collected by the power grid using vulnerabilities in power grid state estimation, resulting in erroneous judgments made by the power grid control center. As a symmetrical defense scheme, FDIA detection usually
[...] Read more.
False data injection attack (FDIA) is a deliberate modification of measurement data collected by the power grid using vulnerabilities in power grid state estimation, resulting in erroneous judgments made by the power grid control center. As a symmetrical defense scheme, FDIA detection usually uses machine learning methods to detect attack samples. However, existing detection models for FDIA typically require large-scale training samples, which are difficult to obtain in practical scenarios, making it difficult for detection models to achieve effective detection performance. In light of this, this paper proposes a novel FDIA sample generation method to construct large-scale attack samples by introducing a hybrid Laplacian model capable of accurately fitting the distribution of data changes. First, we analyze the large-scale power system sensing measurement data and establish the data distribution model of symmetric Laplace distribution. Furthermore, a hybrid Laplace-domain symmetric distribution model with multi-dimensional component parameters is constructed, which can induce a deliberate deviation in the state estimation from its safe value by injecting into the power system measurement. Due to the influence of the multivariate parameters of the hybrid Laplace-domain distribution model, the sample deviation generated by this model can not only obtain an efficient attack effect, but also effectively avoid the recognition of the FDIA detection model. Extensive experiments are carried out over IEEE 14-bus and IEEE 118-bus test systems. The corresponding results unequivocally demonstrate that our proposed attack method can quickly construct large-scale FDIA attack samples and exhibit significantly higher resistance to detection by state-of-the-art detection models, while also offering superior concealment capabilities compared to traditional FDIA approaches.
Full article
(This article belongs to the Special Issue Security, Communication and Privacy in Internet of Things: Symmetry and Advances — Volume II)
►▼
Show Figures
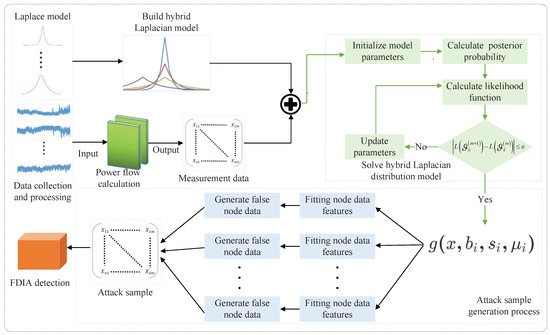
Figure 1
Open AccessArticle
On Cyclic LA-Hypergroups
Symmetry 2023, 15(9), 1668; https://doi.org/10.3390/sym15091668 - 30 Aug 2023
Abstract
Symmetries in the context of hypergroups and their generalizations are closely related to the algebraic structures and transformations that preserve certain properties of hypergroup operations. Symmetric LA-hypergroups are indeed commutative hypergroups. This paper considers a category of cyclic hyperstructures called the cyclic LA-semihypergroup
[...] Read more.
Symmetries in the context of hypergroups and their generalizations are closely related to the algebraic structures and transformations that preserve certain properties of hypergroup operations. Symmetric LA-hypergroups are indeed commutative hypergroups. This paper considers a category of cyclic hyperstructures called the cyclic LA-semihypergroup that is a conception of LA-semihypergroups and cyclic hypergroups. We inaugurate the idea of cyclic LA-hypergroups. The interconnected notions of single-power cyclic LA-hypergroups, non-single power cyclic LA-hypergroups and some of their properties are explored.
Full article
Open AccessArticle
A Relationship between the Schrödinger and Klein–Gordon Theories and Continuity Conditions for Scattering Problems
by
and
Symmetry 2023, 15(9), 1667; https://doi.org/10.3390/sym15091667 - 29 Aug 2023
Abstract
A rigorous analysis is undertaken based on the analysis of both Galilean and Lorentz (Poincaré) invariance in field theories in general in order to (i) identify a unique analytical scheme for canonical pairs of Lagrangians, one of them having Galilean, the other one
[...] Read more.
A rigorous analysis is undertaken based on the analysis of both Galilean and Lorentz (Poincaré) invariance in field theories in general in order to (i) identify a unique analytical scheme for canonical pairs of Lagrangians, one of them having Galilean, the other one Poincaré invariance; and (ii) to obtain transition conditions for the state function purely from Hamilton’s principle and extended Noether’s theorem applied to the aforementioned symmetries. The general analysis is applied on Schrödinger and Klein–Gordon theory, identifying them as a canonical pair in the sense of (i) and exemplified for the scattering problem for both theories for a particle beam against a potential step in order to show that the transition conditions that result according to (ii) in a ‘natural’ way reproduce the well-known ‘methodical’ continuity conditions commonly found in the literature, at least in relevant cases, closing a relevant argumentation gap in quantum mechanical scattering problems.
Full article
(This article belongs to the Special Issue Symmetry and Asymmetry in Quantum Mechanics)
►▼
Show Figures
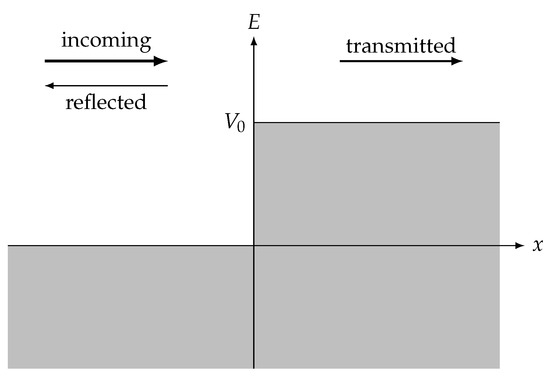
Figure 1
Open AccessArticle
Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative
Symmetry 2023, 15(9), 1666; https://doi.org/10.3390/sym15091666 - 29 Aug 2023
Abstract
In this paper, we propose two efficient methods for solving the fractional-order Schrödinger–KdV system. The first method is the Laplace residual power series method (LRPSM), which involves expressing the solution as a power series and using residual correction to improve the accuracy of
[...] Read more.
In this paper, we propose two efficient methods for solving the fractional-order Schrödinger–KdV system. The first method is the Laplace residual power series method (LRPSM), which involves expressing the solution as a power series and using residual correction to improve the accuracy of the solution. The second method is a new iterative method (NIM) that simplifies the problem and obtains a recursive formula for the solution. Both methods are applied to the Schrödinger–KdV system with fractional derivatives, which arises in many physical applications. Numerical experiments are performed to compare the accuracy and efficiency of the two methods. The results show that both methods can produce highly accurate solutions for the fractional Schrödinger–KdV system. However, the new iterative method is more efficient in terms of computational time and memory usage. Overall, our study demonstrates the effectiveness of the residual power series method and the new iterative method in solving fractional-order Schrödinger–KdV systems and provides a valuable tool for researchers and practitioners in applied mathematics and physics.
Full article
(This article belongs to the Section Mathematics and Symmetry/Asymmetry)
►▼
Show Figures
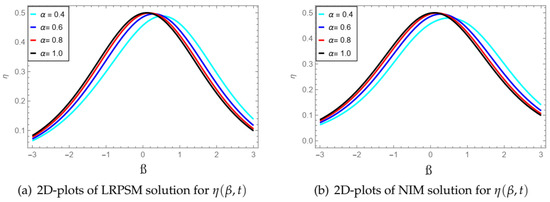
Figure 1
Open AccessArticle
Fixed Point Theorems in Symmetric Controlled M-Metric Type Spaces
Symmetry 2023, 15(9), 1665; https://doi.org/10.3390/sym15091665 - 29 Aug 2023
Abstract
One of the frequently studied approaches in metric fixed-point theory is the generalization of the used metric space. Under this approach, in this study, we introduce a new extension of M-metric spaces, called controlled M-metric spaces, achieved by modifying the triangle
[...] Read more.
One of the frequently studied approaches in metric fixed-point theory is the generalization of the used metric space. Under this approach, in this study, we introduce a new extension of M-metric spaces, called controlled M-metric spaces, achieved by modifying the triangle inequality and keeping the symmetric condition of the space. The investigation focuses on exploring fundamental properties of this newly defined space, incorporating topological aspects. Several fixed-point theorems and fixed-circle results are established within these spaces complemented by illustrative examples to demonstrate the implications of our findings. Moreover, we present an application involving high-degree polynomial equations.
Full article
(This article belongs to the Special Issue Symmetry Application in Fixed Point Theory)
Open AccessFeature PaperArticle
On Ulam Stability with Respect to 2-Norm
Symmetry 2023, 15(9), 1664; https://doi.org/10.3390/sym15091664 - 29 Aug 2023
Abstract
The Ulam stability of various equations (e.g., differential, difference, integral, and functional) concerns the following issue: how much does an approximate solution of an equation differ from its exact solutions? This paper presents methods that allow to easily obtain numerous general Ulam stability
[...] Read more.
The Ulam stability of various equations (e.g., differential, difference, integral, and functional) concerns the following issue: how much does an approximate solution of an equation differ from its exact solutions? This paper presents methods that allow to easily obtain numerous general Ulam stability results with respect to the 2-norms. In four examples, we show how to deduce them from the already known outcomes obtained for classical normed spaces. We also provide some simple consequences of our results. Thus, we demonstrate that there is a significant symmetry between such results in classical normed spaces and in 2-normed spaces.
Full article
(This article belongs to the Special Issue Symmetry in Functional Equations and Inequalities: Volume 2)
Open AccessArticle
Landauer’s Princple for Fermionic Fields in One-Dimensional Bags
Symmetry 2023, 15(9), 1663; https://doi.org/10.3390/sym15091663 - 28 Aug 2023
Abstract
In recent years, growing interest has been paid to the exploration of the concepts of entropy, heat and information, which are closely related to the symmetry properties of the physical systems in quantum theory. In this paper, we follow this line of research
[...] Read more.
In recent years, growing interest has been paid to the exploration of the concepts of entropy, heat and information, which are closely related to the symmetry properties of the physical systems in quantum theory. In this paper, we follow this line of research on the the validity of the concepts in quantum field theory by studying Landauer’s principle for a Dirac field interacting perturbatively with an Unruh–DeWitt detector in a
(This article belongs to the Section Physics and Symmetry/Asymmetry)
►▼
Show Figures
Figure 1

Journal Menu
► ▼ Journal Menu-
- Symmetry Home
- Aims & Scope
- Editorial Board
- Reviewer Board
- Topical Advisory Panel
- Instructions for Authors
- Special Issues
- Topics
- Sections & Collections
- Article Processing Charge
- Indexing & Archiving
- Editor’s Choice Articles
- Most Cited & Viewed
- Journal Statistics
- Journal History
- Journal Awards
- Conferences
- Editorial Office
Journal Browser
► ▼ Journal BrowserHighly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Topic in
Machines, Micromachines, Remote Sensing, Sustainability, Symmetry, Wind
Energy Equipment and Condition Monitoring
Topic Editors: Zhifeng Xiao, Bin Huang, Lida LiaoDeadline: 15 September 2023
Topic in
Axioms, Computation, Dynamics, Mathematics, Symmetry
Structural Stability and Dynamics: Theory and Applications
Topic Editors: Harekrushna Behera, Chia-Cheng Tsai, Jen-Yi ChangDeadline: 30 September 2023
Topic in
Applied Sciences, Diagnostics, Healthcare, IJERPH, Symmetry
Artificial Intelligence in Healthcare - 2nd Volume
Topic Editors: Keun Ho Ryu, Nipon Theera-UmponDeadline: 31 October 2023
Topic in
Entropy, Galaxies, Quantum Reports, Symmetry, Universe
Covariance, Objectivity and Evolution Equations in Either Classical or Quantum Gravity and Quantum Mechanics
Topic Editors: Massimo Tessarotto, Claudio CremaschiniDeadline: 20 November 2023

Conferences
27 October–10 November 2023
The 4th International Electronic Conference on Applied Sciences (ASEC2023)

Special Issues
Special Issue in
Symmetry
Exploring Inter- and Intramolecular Interactions as Building Blocks of Larger Systems II
Guest Editor: Aneta JezierskaDeadline: 1 September 2023
Special Issue in
Symmetry
Nonlinear Nano-Optics
Guest Editors: Thierry Verbiest, Branko Kolaric, Sébastien R. MouchetDeadline: 15 September 2023
Special Issue in
Symmetry
Modified Gravity Theories and Applications to Astrophysics and Cosmology
Guest Editors: Luis Acedo, Michael M. Tung, Golden Gadzirayi NyambuyaDeadline: 30 September 2023
Special Issue in
Symmetry
Symmetry in Advances of Constituent Quark Models
Guest Editor: Chunsheng AnDeadline: 15 October 2023
Topical Collections
Topical Collection in
Symmetry
Symmetry in Ordinary and Partial Differential Equations and Applications
Collection Editor: Calogero Vetro